Functional Encryption 101: Into the Black Box

Functional encryption can often feel like stepping into a dense forest of symbols, equations and abstract definitions. When I first started going through the paper, “Functional Encryption: Definitions and Challenges” by Dan Boneh, Amit Sahai and Brent Waters, I felt like it was in a language that was just beyond my reach. If you have ever felt that way, this post is for you.

This blog is a guided tour where we will walk through the paper together, unpacking the notations, highlighting the big ideas and delving deeper where things get tricky. Whether you are new to functional encryption or just need a quick refresher, you are in the right place.

Let’s get started!

Introduction into the Formal Language and Syntax Used

In the last post, we covered the basics of Functional Encryption. If you are new, start here.

Section 1 of the paper outlines the history and motivation, which I recommend skimming for context. Here, we’ll dive into the formal language and syntax, breaking down the notation and definitions to make them easier to follow.

A functional encryption scheme is governed by four core algorithms:

1. Setup: It generates the public key (aka public parameters, pp) and the master key (mk). As we know, the public parameters are available to everyone, while the master key is kept secret by the trusted party.
2. KeyGen (Key Generation): It uses the master key to generate the secret key (sk) tied to a particular function. This is the reason functional encryption works, i.e. being able to exact only a function of the data without decrypting the data itself.
3. Enc (Encryption): It encrypts the data with the public parameters, to produce the ciphertext.
4. Dec (Decryption): It uses the secret key on the ciphertext to produce the function of the data (y).

These are some of the terms often used in the definitions:

1. Key Space (K): It is the set of all valid keys for a particular scheme.
2. Plaintext Space (X): It is the set of all valid plaintext values for a particular scheme.
3. Security parameter (λ): It controls how hard the scheme is to break. It is usually denoted by 1^λ, which basically means the maximum length is 1^λ. This is done to avoid the confusion that λ itself is the maximum length.
4. Deterministic Turing Machine: It is a theoretical computational model that is predictable. When given a particular input, it will always produce the same output in the same number of steps. When a scheme is represented by a deterministic Turing machine, it is said to be precise and well-defined. We won’t be covering Turing machines here as it is a vast topic that would need its own post.
5. Probabilistic Polynomial Time (PPT) Algorithm: This means the algorithms are both efficient and secure. Probabilistic means that they use randomness to make decisions. For example, flipping a coin to make a decision. Polynomial time means that even if the input size increases, the algorithm will still be able to complete in a reasonable amount of time (not infinitely running).
6. Empty key ($\epsilon$): It is a special non-existent key, used to denote analyse what information about the plaintext the ciphertext leaks.

Now that we have a basic grasp of the language and notation, let’s dive into the key ideas introduced in the paper.

Formal Definitions

Definition 1:

A functionality F defined over (K, X) is a function $F : K \times X \to \{0, 1\}$ described as a (deterministic) Turing Machine. The set K is called the key space and the set X is called the plaintext space. We require that the key space K contain a special key called the empty key denoted $\epsilon$.

Definition 2:

A functional encryption scheme (FE) for a functionality F defined over (K, X) is a tuple of four PPT algorithms (setup, keygen, enc, dec) satisfying the following correctness condition for all k ∈ K and x ∈ X:

1. Generate a public and master secret key pair: $(pp, mk) \leftarrow setup(1^λ)$
2. Generate secret key for k: $sk \leftarrow keygen(mk, k)$
3. Encrypt message x: $c \leftarrow enc(pp, x)$
4. Use sk to compute F(k, x) from c: $y \leftarrow dec(sk, c)$

then we require that y = F(k, x) with probability 1.

If we now apply this to public key encryption (which we discussed in the last blog)

Let K := $\{1, \epsilon\}$ and consider the following functionality F defined over (K, X) for some plaintext space X:

As we know, there is no logic of functions in the general public key encryption scheme. So, we are just considering two cases, k = 1 when the message gets decrypted and k = $\epsilon$, where only length of the decrypted message is revealed, nothing more.

The last part in this section speaks about parameterisation. While we treated K and X as fixed spaces, they often depend on additional information from the Setup algorithm. For example, in RSA, Setup returns a modulus N, and the keys and plaintexts are defined over $Z_N$. So, Setup doesn't just create keys. It also defines the environment they operate in.

Note: $Z_N$ means a set of all integers that can be produced by modulo N

Classes and Sub-classes of Functional Encryption

Now that we understand the basic building blocks of Functional Encryption, it’s time to zoom out a little. Functional Encryption isn’t one single scheme. Depending on what kind of functions the keys can compute, FE branches into different classes and sub-classes. Some allow simple checks, others handle complex computations.

In this section, we’ll look at the main classes introduced in the paper and how they differ.

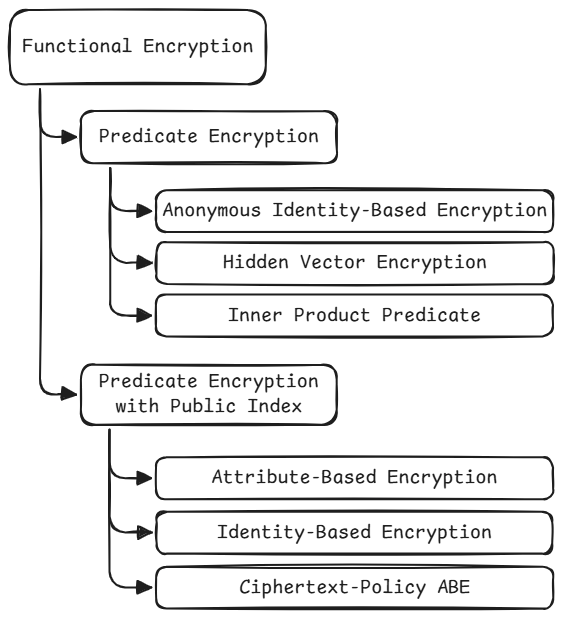
Predicate Encryption

Predicate encryption is a class of functional encryption where the function is a yes/no question (called a predicate).

Unlike regular encryption techniques where m is the plaintext, here the plaintext exists as a pair, (ind, m) ∈ I x M. The index (ind) refers to the label describing the message, which is used to decide if a secret key should work on the ciphertext and m refers to the message. The key is tied to a predicate, P, which decides whether the ciphertext with a given index should be deciphered or not.

If P(k,ind)=1, i.e. the predicate matches the index, decryption succeeds and reveals the message m. If P(k,ind)=0, i.e. the predicate and the index don't match, decryption fails and reveals nothing about m.

Thus, this FE scheme can be defined as a polynomial-time predicate $P : K \times I \to \{0, 1\}$. The FE functionality over $(K \cup \{\epsilon\}, (I \times M))$ is defined as

Let's look at an example:

Suppose we have ind = “Alice” and some message m. Let us assume that our predicate key is “Is the sender = “Alice”?”.

In this case, we will get the decrypted message as m. But, if ind = “Bob”, we would learn nothing about m.

A variation to this is predicate encryption with public index, where instead of keeping the index secret, we reveal it to the user as a publicly known value. In fact, it is explicitly sent with the ciphertext.

One question you might have here is, “Why should index be publicly known? Isn't it a security risk?”

The reason for revealing the index is done as a trade-off. Hidden index value can often lead to heavy cryptographic operations and can be computationally expensive. This is unnecessary in case of operations like sorting, searching, etc., where the goal is to perform these operations on encrypted data and not necessarily focused on finding the right index value.

It's also important to note here that although the index value is leaked, it isn't possible to decrypt data using this information. The only thing we learn is, for example, the identity of the sender, nothing more.

Depending on the type of predicate, we can further divide this into distinct sub-classes. Let’s examine each in detail.

Identity Based Encryption

Here, the predicate is an equality test to verify the identity of the ciphertext.

For key space $K := \{0, 1\}^* \cup \{\epsilon\}$ and a plaintext pair (ind, m), where the index space is $I := \{0, 1\}^*$, the predicate P on $K \times I$ is defined as:

We exclude $\epsilon$ here because it doesn't make sense to have the index as $\epsilon$.

Let’s take an example to understand this better.

Assume ind = “Alice” for a given message m and together they make the plaintext = (“Alice”, m). The sender, Bob, encrypts the plaintext using pp and sends the ciphertext to Alice. Alice authenticates herself by generating a secret key sk = keygen(msk, “Alice”) using the private key generator (PKG).

While decrypting, Alice provides her secret key along with the ciphertext. At this moment, Alice’s identity is verified to make sure that she is the rightful receiver of the message and the decrypted message is outputted.

Anonymous Identity Based Encryption

It is an identity based encryption, except that here, the index is kept private. Hence, the only thing leaked is the length of the message.

Attribute Based Encryption

Here, the predicate is a complex access policy which is used to determine if the access can be granted.

There are 2 types:

1. Key policy ABE:

   In very simple terms, consider a vector $z = (z_1, z_2, z_3, …, z_n)$. This vector is the index, which along with the message forms the plaintext pair, (ind = z, m). The key on the other hand carries the formula. When both the key and index are put together and evaluated, if the output is 1, access is granted and the message can be decrypted. Else, access denied and the message can’t be decrypted.

   Let’s take an example to visualise it.

   Let’s assume three characteristics that help me identify the receiver, Alice:

   1. Is she a student?
   2. Does she study Cryptography?
   3. Is she a faculty?

   The answer to these questions forms my vector z, and hence the value of index, which let’s assume in this case corresponds to (1, 1, 0). When Alice frames the boolean formula, she is sure that she can satisfy both being a student and that she studies cryptography and hence it looks like this: z_Student ​∧ z_Cryptography. Now, if you substitute the value of the vector into the formula, you get 1, meaning access granted. And hence the decryption is successful. Suppose, Alice was a faculty, this would clearly fail.

   Now, one question you might have here is if the index is publicly known and if the receiver requests for the secret key from the PKG by giving the boolean formula as input, then how is this scheme secure? Because in that case, I could look at the value of the index and generate the boolean formula and hence get the perfect secret key that will grant access.

   Here is a slight subtlety that is important to understand. The receiver doesn’t get the encrypted data and hence the value of the index until they generate the secret key from the PKG. And the receiver can only generate the secret key once. Now the scheme is secure, isn’t it?

   We can describe this system for the predicate $P_n: K \times I \to \{0,1\}$, where:

   1. The key space $K$ is the set of all poly-sized boolean formulas $\phi$ in $n$ variables $z = (z_1, \dots, z_n) \in \{0, 1\}^n$. Let $\phi(z)$ be the evaluation of the formula $\phi$ at input $z$.
   2. The plaintext is a pair $(\text{ind} = z, m)$, where the index space is $I := \{0, 1\}^n$ and $z$ is a bit vector $(z_1, \dots, z_n)$.
   3. The predicate $P_n$ on $K \times I$ is defined as:
   $$P_n(\phi \in K, \text{ind} = z \in I) := \begin{cases} 1 & \text{if } \phi(z) = 1 \\ 0 & \text{otherwise} \end{cases}$$

   The same can also be applied using strings instead of bit vectors.

   Note that the boolean formula is a monotone, meaning that only AND and OR are allowed. NOT is not allowed.

2. Ciphertext-Policy ABE:

   This is just the reverse of Key-Policy ABE. Here, the index is the boolean function, i.e., $\text{ind} = \phi$, and the key carries the vector $z$. Everything else is exactly the same.

   We can describe this system for the predicate $P_n: K \times I \to \{0,1\}$, where:

   1. The key space $K := \{0, 1\}^n$ is the set of all $n$-bit strings, representing $n$ boolean variables $z = (z_1, \dots, z_n) \in \{0, 1\}^n$.
   2. The plaintext is a pair $(\text{ind} = \phi, m)$, where the index space $I$ is the set of all poly-sized boolean formulas $\phi$ over $n$ variables.
   3. The predicate $P_n$ on $K \times I$ is defined as:
   $$P_n(z \in K, \text{ind} = \phi \in I) := \begin{cases} 1 & \text{if } \phi(z) = 1 \\ 0 & \text{otherwise} \end{cases}$$

Hidden Vector Encryption

Here, the key essentially checks if the index follows a particular pattern, which becomes the basis for granting access. For the plaintext pair, we have the index represented as a vector and the message itself, i.e., $\text{plaintext} = (\text{ind} = (w_1, \dots, w_n), m)$. The key resembles a regex-like format to pattern-match the index. If the pattern matches, access is granted. This gives more flexibility in how the index should look and makes writing the rule a lot easier.

In this system, a ciphertext has a vector of $n$ elements in $\{0, 1\}^*$, and a private key consists of a vector of $n$ elements in $\{*\} \cup \{0, 1\}^*$, where * is a wildcard character. The key space is $K = (v_1, \dots, v_n)$, where each $v_i \in \{*\} \cup \{0, 1\}^*$. The plaintext is a pair $(\text{ind} = (w_1, \dots, w_n), m)$, where each $w_i \in \{0, 1\}^*$ and the index space is $I := (\{0, 1\}^*)^n$.

Then, the predicate $P_n$ on $K \times I$ is defined as:

Since ind is hidden here, only the length of the message is revealed.

Hidden vector encryption enables fine-grained searches, such as conjunctive queries and range queries, without revealing the underlying attribute values.

Inner Product Predicate

To understand inner product predicate, we first need to understand what ring and field means and how they are different, and to understand that, we need to understand additive and multiplicative inverse. So, let’s start from that.

Additive inverse in cryptography is almost the same as what it means in math, but with a small twist.

Remember we learnt the idea of $Z_n$ while defining the definition of functional encryption. We will bring that back here. So, anytime we want to calculate the additive inverse of any number, we say we want the additive inverse of that number in Z_n. It would be easier to explain this with an example.

Let’s consider $Z_5$. $Z_5$ contains possible results of mod 5, which means

Suppose, we have to find the additive inverse of 1. According to the definition, I need to find the value, which when added to 1 gives 0, which is -1 in math. However, there is one small issue: Subtraction and division are invalid operations in cryptography, which means negative numbers are out of the question. But, lucky for us, mod comes to save the day.

In cryptography, we modify the definition of additive inverse as:

Using this new definition, the additive inverse of 1 over $Z_n$ becomes 4 as (1+4) mod 5 = 0.

Similarly, the new definition of multiplicative inverse becomes:

But, one issue with multiplicative inverse is that not all integers in $Z_n$ may have a multiplicative inverse.

Let’s consider $Z_8$.

Here, 2 doesn’t have a multiplicative inverse as product mod 8 never gives 1.

With this information, we can now define a ring and a field. Ring means that the additive and multiplicative inverse may not be in $Z_n$. Field means that the additive and multiplicative inverse must be in $Z_n$.

Initially the inner product predicate was defined over a ring $Z_n$. But, given that additive and multiplicative inverses may or may not exist, it complicates proofs. Hence, we define it over a $F_p$, where p is a prime number (mod prime is always a field).

The idea of inner product predicate is simple. We set up a dot product expression to evaluate any function we need to compute. This allows us to perform complex evaluations like disjunction, CNF (Conjunctive Normal Form), DNF (Disjunctive Normal Form), polynomial, etc. Both the key and the index here are vectors and access is granted if their dot product gives the result as 0.

The scheme is defined as:

1. The setup algorithm defines a randomly chosen prime $p$ of length $\kappa$, where $\kappa$ is the security parameter.
2. The key space $K$ is all $\vec{v} = (v_1, \dots, v_n)$ where each $v_i \in \mathbb{F}_p$.
3. The plaintext is a pair $(\text{ind} = (w_1, \dots, w_n), m)$ where each $w_i \in \mathbb{F}_p$. The index space is $I := (\mathbb{F}_p)^n$.
4. The predicate $P_{n,p}$ on $K \times I$ is defined as: $$P_{n,p}\left( (v_1, \dots, v_n) \in K, \text{ind} = (w_1, \dots, w_n) \right) := \begin{cases} 1 & \text{if } \sum_{i=1}^{n} v_i \cdot w_i = 0 \\ 0 & \text{otherwise} \end{cases}$$

Other systems

By using a combination of systems, we can make new systems. Some examples are:

1. Attribute-Based Encryption and Broadcast Encryption
2. Identity-Based Broadcast Encryption
3. Broadcast HIBE
4. Inner-Product Encryption and ABE

Conclusion

Through this blog, we moved beyond the simple “dot product” view and uncovered the bigger picture of functional encryption and its subclasses. What began as a small, simple idea has now taken shape into a clear, well-defined concept.

If this post felt heavier or denser than the last one, that’s completely natural—you are encountering a lot of notation and theory for the first time. But I hope that as we went along, the pieces started clicking into place and felt easier to grasp.

And remember, this isn’t the finish line. The real question still lingers: are these encryption schemes truly secure? That’s the mystery we’ll unravel next in our deep dive into security definitions.